Electrical Circuits: Impedance and Admittance

IMPEDANCE AND ADMITTANCE

What is Impedance ?

While Ohm's Law applies directly to resistors in DC or in AC circuits, the form of the current-voltage relationship in AC circuits in general is modified to the form:

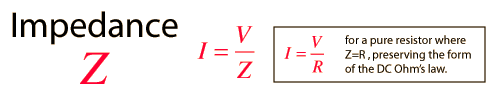
where I and V are the rms or "effective" values. The quantity Z is called impedance. For a pure resistor, Z = R. Because the phase affects the impedance and because the contributions of capacitors and inductors differ in phase from resistive components by 90 degrees, a process like vector addition (phasors) is used to develop expressions for impedance. More general is the complex impedancemethod.

Impedance Combinations

Combining impedances has similarities to the combining of resistors, but the phaserelationships make it practically necessary to use the complex impedance method for carrying out the operations. Combining series impedances is straightforward:

Calculation

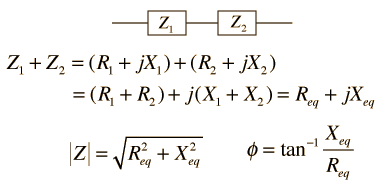Combining parallel impedances is more difficult and shows the power of the complex impedance approach. The expressions must be rationalized and are lengthy algebraic forms.

Expressions

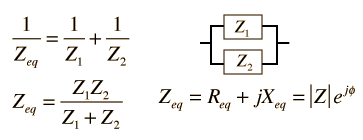What is Admittance ?

In electrical engineering, admittance is a measure of how easily a circuit or device will allow a current to flow. It is defined as the inverse of impedance. The SI unit of admittance is the siemens (symbol S). Oliver Heaviside coined the term admittance in December 1887.^[1]

Admittance is defined as

Y \equiv \frac{1}{Z} \,

where

Y is the admittance, measured in siemens

Z is the impedance, measured in ohms

The synonymous unit mho, and the symbol ℧ (an upside-down uppercase omega Ω), are also in common use.

Resistance is a measure of the opposition of a circuit to the flow of a steady current, while impedance takes into account not only the resistance but also dynamic effects (known as reactance). Likewise, admittance is not only a measure of the ease with which a steady current can flow, but also the dynamic effects of the material's susceptance to polarization:

Y = G + j B \,

where

$Y$ is the admittance, measured in siemens.
$G$ is the conductance, measured in siemens.
$B$ is the susceptance, measured in siemens.
$j^2 = -1$

Conversion from impedance to admittance

The impedance, Z, is composed of real and imaginary parts,

Z = R + jX \,

where

R is the resistance, measured in ohms
X is the reactance, measured in ohms

Y = Z^{-1}= \frac{1}{R + jX} = \left( \frac{1}{R^2 + X^2} \right) \left(R - jX\right)

Admittance, just like impedance, is a complex number, made up of a real part (the conductance, G), and an imaginary part (the susceptance, B), thus:

Y = G + jB \,\!

where G (conductance) and B (susceptance) are given by:

\begin{align} G &= \Re(Y) = \frac{R}{R^2 + X^2} \\ B &= \Im(Y) = -\frac{X}{R^2 + X^2} \end{align}

The magnitude and phase of the admittance are given by:

\begin{align} \left | Y \right | &= \sqrt{G^2 + B^2} = \frac{1}{\sqrt{R^2 + X^2}} \\ \angle Y &= \arctan \left( \frac{B}{G} \right) = \arctan \left( -\frac{X}{R} \right) \end{align}

where

G is the conductance, measured in siemens
B is the susceptance, also measured in siemens

Note that (as shown above) the signs of reactances become reversed in the admittance domain; i.e. capacitive susceptance is positive and inductive susceptance is negative.

Overview and Insights

In this topic I learned about the steps you need to follow in order to use the formula. The larger C the more movement of charge the smaller resistance. The higher F the more movement of charge approaching short-circuit.

Electrical Circuits

Mga Pahina

Martes, Disyembre 30, 2014

Impedance and Admittance

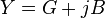
Walang komento:

Mag-post ng isang Komento